নির্ভরণ সমীকরণ এবং নির্ভরণ রেখা (Equation of Line and Line Equation) গণিতের গুরুত্বপূর্ণ ধারণা, যা জ্যামিতি ও বিশ্লেষণমূলক জ্যামিতিতে ব্যাপকভাবে ব্যবহৃত হয়। এখানে নির্ভরণ সমীকরণ এবং নির্ভরণ রেখার বিস্তারিত আলোচনা দেওয়া হলো।

নির্ভরণ সমীকরণ

নির্ভরণ সমীকরণ হলো একটি রেখার গাণিতিক উপস্থাপন, যা নির্দিষ্ট বিন্দু বা শর্ত পূরণ করে। দুই মাত্রার 2D সমতলে একটি রেখা x এবং \y-এর মধ্যে সম্পর্ক স্থাপন করে। এটি সাধারণত দুটি রূপে প্রকাশ করা হয়:

১. ঢাল-কেটে রূপ (Slope-Intercept Form)

এখানে,

• mহলো রেখার ঢাল slope।
• c হলো y-অক্ষের উপর রেখার ছেদ বিন্দু y-intercept।

২. সাধারণ রূপ (General Form)

Ax + By + C = 0
এখানে, A, B, এবং C হলো ধ্রুবক (constants)।

নির্ভরণ রেখা

নির্ভরণ রেখা হলো একটি সরলরেখা, যা নির্ভর করে সমীকরণের ধ্রুবক গুণাগুণের উপর। এটি সমতলে xও y-এর সম্পর্ক প্রদর্শন করে। রেখা বিভিন্ন শর্তে ভিন্ন রূপে প্রকাশিত হয়:

১. ঢাল নির্ণয়

২. বিন্দু-ঢাল রূপ (Point-Slope Form)

৩. দুই বিন্দুর রূপ (Two-Point Form)

৪. অনুভূমিক রেখা (Horizontal Line)

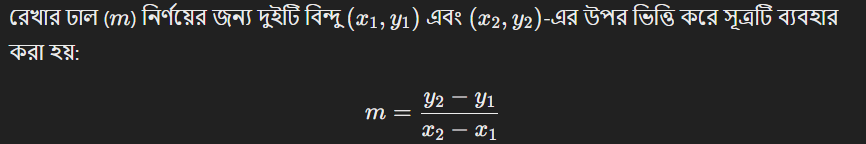
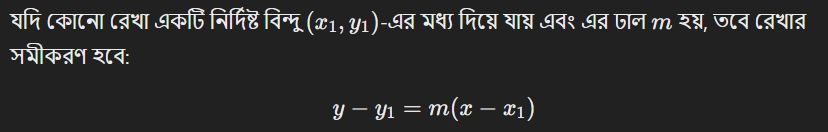
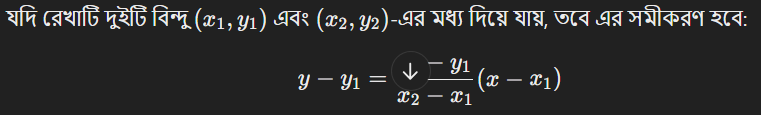
যদি রেখাটি অনুভূমিক হয়, তবে \(y = c\), যেখানে \(c\) হলো \(y\)-অক্ষের উপর রেখার উচ্চতা।

৫. উল্লম্ব রেখা (Vertical Line)

যদি রেখাটি উল্লম্ব হয়, তবে x = k, যেখানে k হলো x-অক্ষের উপর রেখার স্থান।

উদাহরণ

উদাহরণ ১: ঢাল-কেটে রূপ

ধরা যাক, একটি রেখার ঢাল m = 2 এবং y-অক্ষের উপর ছেদ বিন্দু c = -3। রেখার সমীকরণ হবে:

উদাহরণ ২: দুই বিন্দুর রূপ

দুটি বিন্দু \(1, 2) এবং (3, 6) -এর মধ্য দিয়ে যাওয়া রেখার সমীকরণ নির্ণয় করতে:

সারসংক্ষেপ

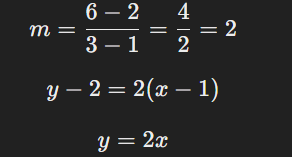
নির্ভরণ সমীকরণ এবং নির্ভরণ রেখা জ্যামিতি ও বিশ্লেষণমূলক গণিতের ভিত্তি। এটি বিভিন্ন রূপে প্রকাশিত হয়, যেমন ঢাল-কেটে রূপ, সাধারণ রূপ, এবং বিন্দু-ঢাল রূপ। রেখার ঢাল, বিন্দু, এবং অবস্থানের ভিত্তিতে এর সমীকরণ নির্ধারণ করা হয়।